2 postulat dalam relativitas khusus

Posted by Ibnu Abdillah

Orang biasa akan bertanya "berapa?", "bagaimana", "dimana",

orang yang lebih cerdas bertanya "mengapa?"

lebih pintar lagi akan bertanya "siapa yang mengatur itu semua?"

Cahaya, atau lebih umum lagi gelombang elektromagnet telah dijabarkan oleh J.C. Maxwell dengan 4 persamaan-nya yang terkenal itu.


Name	Differential form	Integral form
Gauss's law	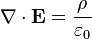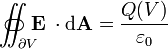$\nabla \cdot \mathbf{E} = \frac {\rho} {\varepsilon_0}$	$\int\!\!\!\!\!\!\!\!\;\!\;\!\subset\;\!\;\!\!\;\!\!\!\!\!\!\!\int_{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\;\!\!\supset \mathbf E\;\cdot\mathrm{d}\mathbf A = \frac{Q(V)}{\varepsilon_0}$
Gauss's law for magnetism	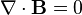$\nabla \cdot \mathbf{B} = 0$	$\int\!\!\!\!\!\!\!\!\;\!\;\!\subset\;\!\;\!\!\;\!\!\!\!\!\!\!\int_{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\;\!\!\supset \mathbf B\;\cdot\mathrm{d}\mathbf A = 0$
Maxwell–Faraday equation (Faraday's law of induction)	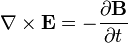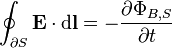$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}$	$\oint_{\partial S} \mathbf{E} \cdot \mathrm{d}\mathbf{l} = - \frac {\partial \Phi_{B,S}}{\partial t}$
Ampère's circuital law (with Maxwell's correction)	$\nabla \times \mathbf{B} = \mu_0\mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}} {\partial t}\$	$\oint_{\partial S} \mathbf{B} \cdot \mathrm{d}\mathbf{l} = \mu_0 I_S + \mu_0 \varepsilon_0 \frac {\partial \Phi_{E,S}}{\partial t}$

tabel 4 persamaan Maxwell dalam bentuk differensial dan integral pada ruang hampa

Salah satu implikasi dari persamaan Maxwell tersebut adalah nilai cepat rambat gelombang elektromagnet yang invarian terhadap perubahan kerangka acuan dalam ruang hampa. Hal ini bertentangan dengan konsep alih-ragam koordinat Galileo yang terdapat di mekanika Newton.

Hanya ada 3 kemungkinan, persamaan Maxwell salah (mekanika newton benar), mekanika Newton salah (Maxwell yang benar, dan diperlukan alih-ragam baru), atau kedua-duanya salah (tetap saja diperlukan alih-ragam baru).

Einstein, pada tahun 1905 menerbitkan papernya yang berjudul "on The Dymanics of Moving Bodies", yang membahas tentang keanehan alih-ragam galileo ini. Ia mengawalinya dengan 2 postulat, yang kemudian dikenal sebagai 2 postulat dalam relativitas khusus, yaitu :

1. Bentuk hukum fisika tidak bergantung pada kerangka acuan inersial yang dipakai (kovariansi hukum fisika)

2. Nilai cepat rambat cahaya dalam ruang hampa selalu bernilai tertentu, tidak bergantung pada kerangka acuan inersialnya (invariansi cepat rambat cahaya)

Lalu apa maksud dari 2 postulat tersebut?

Postulat pertama, secara mudah mengatakan bentuk hukum-hukum fisika yang berlaku pada suatu kerangka acuan inersial akan sama dengan hukum yang berlaku pada kerangka inersial lainnya.

misalnya pada suatu kerangka acuan inersial berlaku hukum kedua newton F=m.a (untuk massa konstan), maka pada kerangka acuan inersial lainnya bentuk persamaannya akan sama hanya saja F'=m'.a', nilai F, m, atau a-nya mungkin berbeda.

Postulat kedua, mungkin agak sulit diterima akal kita yang terlalu alamiah dengan mekanika newton. Pada mekanika Newton yang biasa kita pakai, jika kita mengendarai roket dengan kecepatan 0,5c kemudian memancarkan cahaya (yang memiliki kecepatan c), maka oleh pengamat yang diam dibumi ia akan melihat besar kecepatan cahaya yang kita pancarkan adalah 1,5c.

Namun menurut postulat kedua tersebut (dan secara experimental dibuktikan, juga oleh persamaan Maxwell), besar kecepatan cahaya menurut pengamat diam juga c.

Lalu? apa yang sebernarnya terjadi? kemungkinanya adalah orang di bumi memiliki pengamatan terhadap panjang (jarak) dan waktu yang berbeda dengan pengamat bergerak. Hal ini jelas karena besar kecepatan cayaha ditentukan oleh jarak yang ditempuh dan selang waktu yang diperlukan untuk menempuh jarak itu.

Sebelum Einstein, Voigt, FitzGerald dan Lorentz pernah berpendapat bahwa ada perbedaan panjang dan waktu yang diamati oleh pengamat yang berada pada kerangka inersial yang berbeda. Artinya, alih-ragam yang berbeda untuk perpindahan sistem koordinat. Dalam alih-ragam tersebut antara jarak (secara umum, ruang) tidak lagi terpisah. Tidak lagi ada konsep ruang mutlak dan waktu mutlak. Inilah awal teori Relativitas. Tidak lagi memisahkan ruang dan waktu, melainkan ruang-waktu. tidak lagi 3 dimensi ruang. melainkan 4 dimensi ruang-waktu.

Implikasi selanjutnya, setiap pengamat memiliki sistem koordinatnya sendiri, yang berbeda dengan pengamat lain. Pengamat satu dengan pengamat lain tidak lagi sepakat mengenai pertambahan umur mereka (lihat Paradoks Kembar) dan tidak pula dengan jarak perjalanan tempuh mereka. Massa pun mengalami perbedaan pada pengamatan masing-masing. Kemudian dikenal adanya istilah massa diam dan massa gerak. Bahasan selanjutnya akan diperjelas mengenai ruang-waktu 4 dimensi ini dan mekanikan baru didalamnya.

These icons link to social bookmarking sites where readers can share and discover new web pages.