Soal | Tensor Metrik

Posted by Ibnu Abdillah

Soal ini diambil dari buku Gravity, Black Holes, and the Very Early Universe karangan Chow dkk, ini kebetulan jadi bahan skripsi penulis hehehe. mohon maaf dengan penjelasn seadanya.

Soal :

1.1. By direct transformation from Cartesian coordinates, calculate the metric tensor gμν in a flat three-dimensional space in terms of (a) spherical coordinates and (b) cylindrical coordinates.

Nah untuk membahas soal ini kita harus tahu dulu formulasi elemen garis pada sistem koordinat tersebut.kemudian berdasarkan persamaan

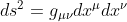
$ds^{2}=g_{\mu \nu} dx^{\mu} dx^{\nu}$

kita bisa tahu matriks gμν nya
Info mengenai elemen garis (line element) bisa di klik di http://en.wikipedia.org/wiki/Line_element

langsung saja bahas soalnya

a. Pada sistem koordinat kulit bola (spherical coordinate) alih-ragam dari kartesian menuju sistem koordinat kulit bola (r, θ, φ ), dengan r ∈ [0, ∞ ), θ ∈ [0, π ], φ ∈ [0, 2π ), adalah

$ds^{2}=(dr)^2+r^2 (d\theta)^2 + r^2 sin^2 \theta (d \varphi)^2$

maka bentuk matrix gμν nya adalah

$g_{\mu \nu} dx^{\mu} dx^{\nu}=\begin{bmatrix} 1 & 0 & 0\\ 0 & r^2 & 0\\ 0 & 0 & r^2 sin^2 \theta \end{bmatrix}$

b. Pada sistem koordinat silinder elemen garisnya

$ds^2 = (dr)^2 + \rho^2 (d \phi)^2 + (dz)^2$

maka bentuk matriknya

$\begin{bmatrix} 1 & 0 & 0\\ 0 & \rho^2 & 0\\ 0 & 0 & 1 \end{bmatrix}$

Gampang kan??

These icons link to social bookmarking sites where readers can share and discover new web pages.